SUPPORT VECTOR MACHINES - All You Need To Know
OBJECTIVE: To obtain a hyperplane that separates the different classes of data-points with maximum margin.
A Support Vector Machine(SVM) is a very powerful and versatile Machine Learning model which is a type of Supervised Machine Learning Algorithm. It is capable of performing linear and non-linear classification, regression, and even outlier detection. It is one of the most popular models in Machine Learning and anyone interested in ML should definitely have it in their toolbox. SVMs are particularly well suited for the classification of complex but small or medium-sized datasets.
This blog will explain the core concepts and the formulations of the SVM models.
The main objective of SVMs is to obtain a Decision Boundary with maximum-margin. Now, what does that mean? Let us understand step by step:
Hyperplanes:
Firstly what is a Hyperplane? You can find a brief introduction here in the image that I posted on my Instagram page (@codingsnap)
Now suppose you are given a dataset with instances belonging to the two different classes. When you plot the data points, you luckily find them to be linearly separable. Now you are to choose a decision boundary that separates the two classes.
There could be multiple boundaries that could classify the data points correctly. But here SVM says that I'll give you that boundary which has the maximum-margin. By maximum-margin it means that the hyperplane not only classifies the points correctly but also remains as far as possible from the nearest instances of both the classes. This type of model performs better on new instances and increases the robustness of the model.
How to approach now? Simple, let us suppose there are two classes positive and negative.
- These classes can be separated by hyperplanes supported by support vectors.
- Let the weight matrix be 'w' and the feature matrix be 'x'.
- The equation of the hyperplane will turn out be 'wTx + b = 0' , where b is the bias.
- The hyperplane supported by the positive instances has the equation 'wTx + b = k' , where k is some positive value(for simple calculation we'll take 1).
- The hyperplane supported by the negative instances has the equation 'wTx + b = -k' , where k is some negative value.
- We already know the objective it is to obtain a maximum-margin hyperplane.
- It can be achieved by maximizing the margin(distance between the positive and negative hyperplanes).
We can achieve our objective by maximizing this distance as much as possible. But there is constraint that should also be followed that the distance should be maximised such that the points are correctly classified. The classification of the point can be given by the equation:
where y is the class positive or the negative class that the data points belong to. w is a matrix of size nx1 and x is the feature matrix of size 1xn, the second term in the bracket gives the scalar output. Therefore, if the point is positive(+1) and correctly classified that means positive multiplied by positive will be equal or greater than 1. If the point is negative(-1) then negative multiplied by negative scalar will also be equal or greater than 1(because x is going to have some negative direction).
Note: We can't directly start applying gradient descent or any other optimization technique on the distance formula, we need to transform it into a differentiable function. Therefore, let's take two points xn and xp and calculate the distance.
Calculating d1 and d2:
We had to maximize 'd', but the same objective can now be achieved by minimizing ||w||. This formulation is called the Hard-margin SVM.
If we strictly impose that all the instances be off the margin then there occur two main issues: Firstly, it only works if the data is linearly separable and secondly it is quite sensitive to the outliers. Hard-margin SVM tends to overfit on the data, as this tries to classify every point correctly thus ending up with a narrow margin.
In real-word, the data is never going to be linearly separable. There has to be some outlier here and there overlapping and making the dataset complex.
In that scenario, hard-margin SVM will underperform.
But still, SVM got our back, with the concepts like Soft-margin SVM and kernel trick it performs outstandingly well.
Soft-Margin Classification
Let us now suppose our dataset contains some outliers, see the figure below
Consider the above cases, which model would you prefer? Obviously, the second one, because it generalizes the model very well to new instances, right?
And this is nothing but the Soft-margin SVM classification. This leniency to tune hard and soft margins are given by a hyper-parameter 'c'.
Formulating equation for soft-max margin:
The value 0.2 is the value by which the incorrect direction of a data point is represented. And this is noted by this symbol: (zeta)
For every point xi the value i is calculated.
Therefore, the equation obtained for soft-max SVM is:
Since, it is a constrained optimization problem, it is hard to optimize directly, as it is also a non-convex function. i.e. When we randomly initialize our algorithm may get stuck in some local minima and we won't get the optimal solution. We can solve this constrained convex optimization problem using any of the three methods:














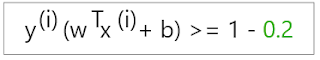




0 Comments